The following theorem is known to me as Elsebe's Theorem.

Elsebe's Theorem has application to TSP routes, because it means that anywhere where two segments of a route intersect, the route can be shortened by substituting the two opposite sides of the quadrangle, rather than using the diagonals.

Note that where two segments intersect, then the end points of the segments make up the quadrangle in question.

The theorem states that the sum of the diagonals of a quadrangle, where the diagonals intersect, are longer than the sum of any of the two opposing sides.

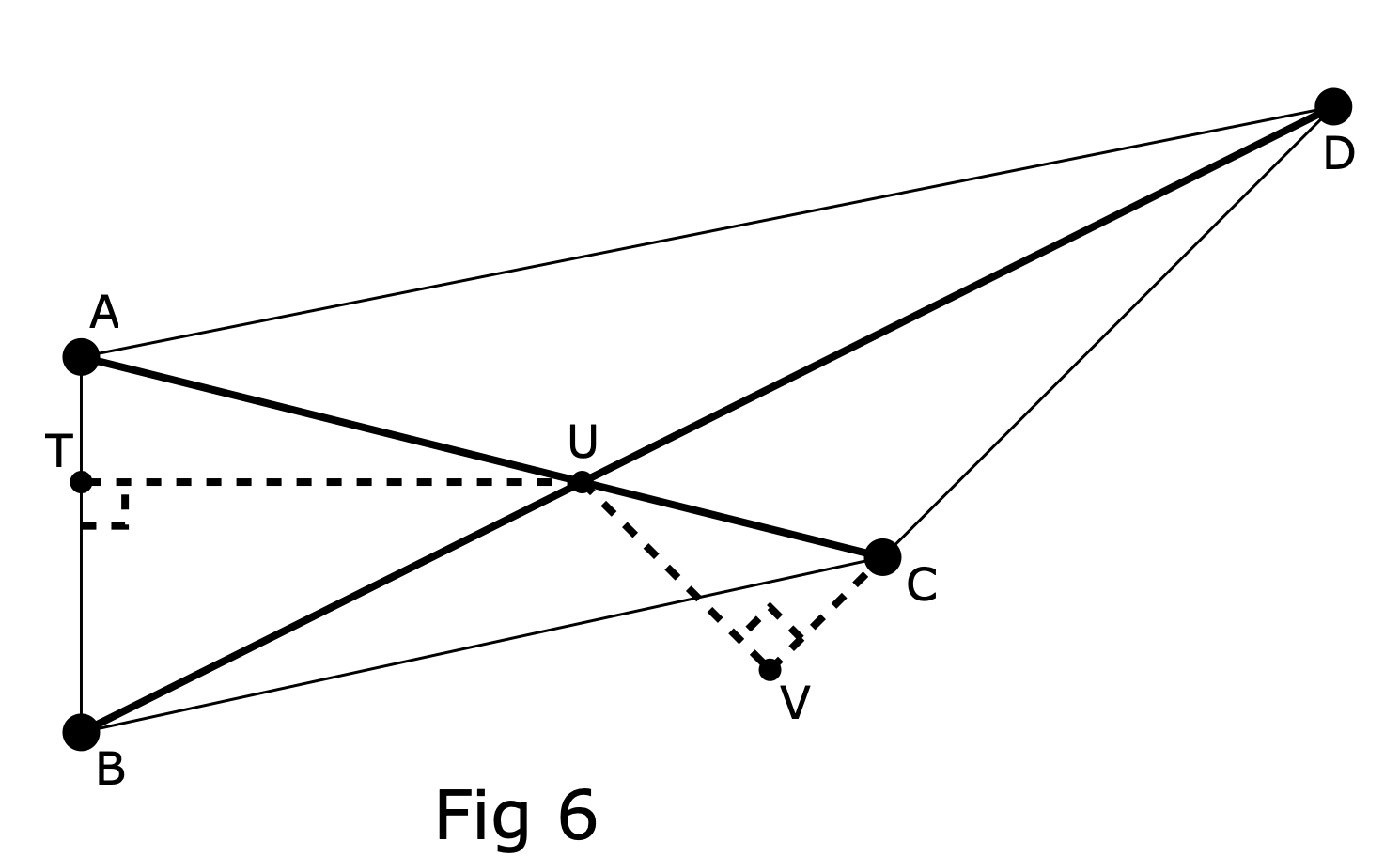
Therefore, for a quadrangle ABCD (refer Fig 6 below), where AC and BD intersect, then-
 
    a) the sum of diagonals AC and BD are greater than
        the sum of the sides AB and CD.
 
    b) the sum of diagonals AC and BD are greater than
        the sum of the sides BC and DA.

The proof of the theorem is as follows-

For a quadrangle ABCD where AC and BD intersect, label the intersection as point U.

Drop a line perpendicular to AB, from U to line AB, and label the intersection on line AB as point T. Where T is between A and B this is known as the inside case.

Drop a line perpendicular to the extension of CD, from U to point V. Where V is not between C and D this is known as the outside case.

For a diagram of points A,B, C, D. T, U and V refer to Fig 6.

Note that ATU and BTU are right angle triangles.
And therefore from Pythagoras we know that-
1    AU > AT ( because AU² = AT² + TU² )
2    BU > BT ( because BU² = BT² + TU² )

Note that CVU and DVU are right angle triangles.
And therefore from Pythagoras we know that-
3    CU > CV ( because CU² = CV² + VU² )
4    DU > DV ( because DU² = DV² + VU² )

From step 1 and 3 above where AU > AT and CU > CV, therefore-
5    AU + CU > AT + CV

Also, from the diagram AC = AU + CU, therefore -
6    AC > AT + CV

From step 2 and 4 above where BU > BT and DU > DV, therefore-
7    BU + DU > BT + DV

Also, from the diagram BD = BU + DU, therefore -
8    BD > BT + DV

Add the inequalities in step 6 and step 8 together -
9    AC + BD > AT + CV + BT + DV

From the drawing showing the inside case-
10    AB = AT + BT (inside case)

From the drawing showing the outside case-
11    DV = CD + CV (outside case)

Note that the example shown (refer Fig 6) includes an inside case for segment AB, and an outside case for segment CD. For quadrangles where both AB and CD segments are inside cases, then use the equation sequence from step 10 onwards for both AB and CD. For quadrangles where both AB and CD segments are outside cases, then use the equation sequence from step 11 onwards for both AB and CD.

From the inequality in step 11-
12    CV = CD + DV

Form the inequality in step 9-
13    AC + BD > (AT+BT) + (CV+DV)

Apply (AT+BT = AB) from step 10 because AB is an inside case, and (CD+CV = DV) from step 12 because CD is an outside case-
14    AC + BD > (AB) + (CV + (CD+CV))

Therefore-
15    AC + BD > AB + CD + 2CV

Therefore, because AB + CD is less than AB + CD + 2CV then-
16    AC + BD > AB + CD

Therefore, for any quadrangle the sum of the diagonals (AC+BD), where the diagonals intersect, are longer than the sum of any of the two opposing sides AB+CD or AD+BC.

Where two segments intersect, the four points of the 2 segments make up a quadrangle. And therefore any of the sum of 2 opposite sides will be less than the diagonals - therefore a TSP route will always be shorter where there are no intersecting segments.

A link to a page about the Theorem idea from Wolfram MathWorld

First disclosed Jan 2022, by Neil William Kirkness, Box 2041 Marmion WA 6020 Australia.